Witam!
Uruchomiłem w mierniku przekaźnik od strony wyjścia sygnału. Wtrąca on w tor pomiarowy tłumienie ok. 30dB "osłabiając" sygnał co opisałem nieco wcześniej w poście #199. Tłumienie można zmniejszyć lub zwiększyć poprzez zmianę opornika mającego na schemacie wartość 1.5k.
Decyzję o wtrąceniu tłumienia podejmuje się na etapie kalibracji ogólnej lub kalibracji SWR. Po wybraniu opcji Pomiar -> Kalibracja lub Pomiar -> Kalibracja SWR pojawi się teraz dodatkowy ekran:
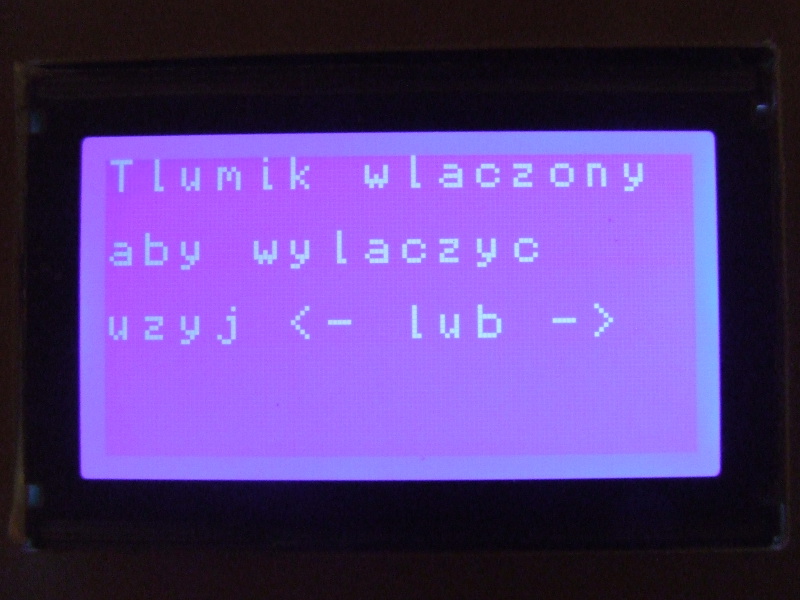
Informuje on o bieżącym stanie tego tłumika i proponuje jego zmianę. Użycie klawisza środkowego (Enter) zachowuje stan aktualny (tłumik włączony lub wyłączony) natomiast użycie jednego z prawych klawiszy (<-) lub (->) spowoduje zmianę stanu tłumika na przeciwny.
Włączenie tłumika zmniejsza dynamikę pomiarową ale pozwala za to na dokładniejszy ogląd charakterystyk w zakresie małego tłumienia. Dla przykładu poniżej dwie charakterystyki drabinkowego filtra kwarcowego mierzone bez tłumienia i z dodatkowym tłumieniem:
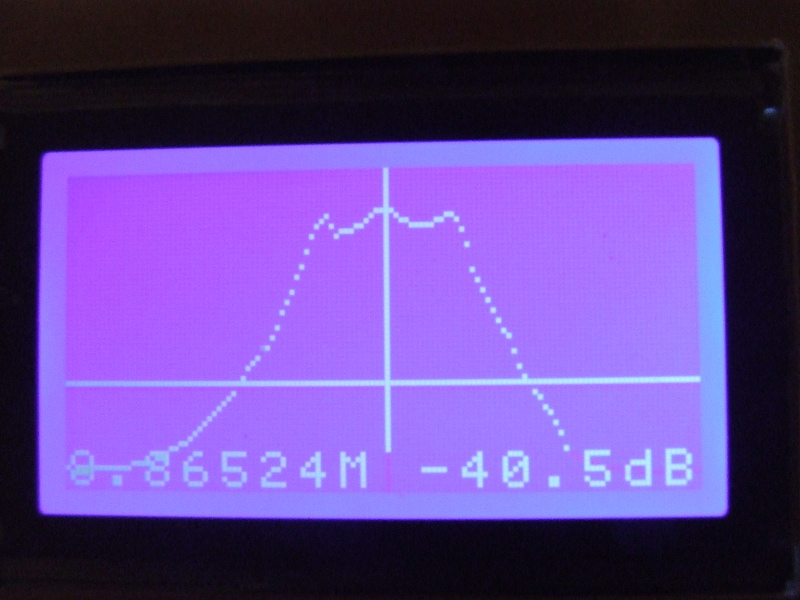

Na obu wykresach zakres przemiatania to ok. 5kHz dla filtra o częstotliwości środkowej 8.8652MHz. Na lewej charakterystyce tłumik jest wyłączony a na prawej włączony. Widać, że na prawym wykresie zafalowanie w paśmie jest większe a zbocza filtra bardziej strome. Pozwala to na optymalizację charakterystyki w paśmie przenoszenia.
Ta funkcjonalność wymaga
nowego oprogramowania w wersji 7.1
i jest to prawdopodobnie ostatnia "większa" poprawka funkcji NA01 z procesorem M32 bo zajętość pamięci procesora to 99%. Podobną funkcjonalność wprowadziłem do miernika NA02 co opiszę oddzielnie a tu chciałbym przy okazji podziękować Markowi SQ7HJB, który testował zmiany oprogramowania na swoim egzemplarzu NA01 bo ja chwilowo takiego nie mam :-( . Przy okazji przypomnę, że mam jeszcze kilka kompletów płytek do NA01 o czym pisałem w poście #199.
W kolejnym poście pokażę metodycznie jak wykorzystując tą i kilka innych funkcjonalności zbudować od podstaw drabinkowy filtr kwarcowy.
L.J.
Witam!
Zgodnie z obietnicą pokażę krok po kroku jak zaprojektować własny filtr kwarcowy. Traktuję mój post po części jako dydaktykę a po części jako prezentację możliwości NA01/02 (na obu miernikach można wykonać podobne czynności) więc proszę znawców tematu o wyrozumiałość. Mam jednak nadzieję, że kilku kolegom przyda się uporządkowana porcja wiadomości na temat metodologii pomiarów jak i podstawowych elementów elektronicznych.
Rezonator kwarcowy to zespół mechaniczno-elektryczny - zwykle to cienka płytka kwarcowa z napylonymi okładzinami - mający tą cechę, że pobudzony impulsem elektrycznym odpowiada mechanicznymi drganiami struktury krystalicznej, które z kolei powodują zmianę potencjału na okładzinach kwarcu. W sprzyjających warunkach, z zastosowaniem elementu aktywnego (tranzystor, lampa) oraz dodatniego sprzężenia zwrotnego można uzyskać ciągłe drgania o częstotliwości określonej właściwościami kwarcu. Istotną cechą tych drgań jest duża stabilność częstotliwości, rzędu 10-6 lub lepiej. Kilka kwarców połączonych szeregowo z dodatkiem kilku elementów pasywnych (zwykle kondensatorów) jest w stanie działać jak wąskopasmowy filtr o małym tłumieniu w paśmie przenoszenia i dużym poza pasmem - to idealne rozwiązanie do celów formowania sygnału SSB.
Analizując rezonator kwarcowy okazało się, że jego analogią może być szeregowy układ rezonansowy o bardzo dużej dobroci. Wnikliwsza analiza doprowadziła do ustalenia modelu zastepczego kwarca jak na poniższym rysunku:
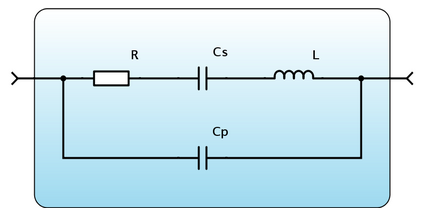
Cs i L to właściwe elementy zastępcze rezonansu szeregowego, Cp to pasożytnicza pojemność równoległa (głównie oprawki kwarcu) a R to zastępcza oporność strat wynikającą głownie z ciepła jakie wydziela się podczas drgań rezonatora. W zastosowanich praktycznych wykorzystuje się rezonans szeregowy Cs i L ale ze względu na pojemność Cp kwarc posiada również rezonans równoległy leżący wyżej od kilkunastu do kilkudziesięciu kilocherców od rezonansu szeregowego. W dalszej części pokażę jak ustalić poszczególne składniki modelu kwarcu do dalszych obliczeń na podstawie pomiarów za pomocą miernika NA01/02.
Budowa filtra kwarcowego - krok 1 - dobór rezonatorów.
Początkowo, należy dobrać kilka rezonatorów kwarcowych o możliwie zbliżonych parametrach - chodzi przede wszystkim o szeregową częstotliwość rezonansową oraz w drugiej kolejności dobroć. Najlepszym rozwiązaniem jest przebranie większego zbioru kwarców w sklepie za zgodą znajomego sprzedawcy. Mierniki NA01/02 nadają się do tego idealnie bo nie wymagają wleczenia ze sobą większego środowiska pomiarowego.

Do pomiarów kwarców należy użyć przystawki LCQ oraz wybrać z menu pomiarowego "Pomiar -> Pomiar + Q". Zakres pomiarowy powinien obejmować spodziewaną częstotliwość rezonansową z niewielkim zakresem poniżej i powyżej - zwykle wystarcza 5 do 10kHz dla całego zakresu przemiatania. Najłatwiej jest to uzyskać wybierając z głównego menu typ pomiaru "DEL" z wartością "DELTA" właśnie 5-10kHz.
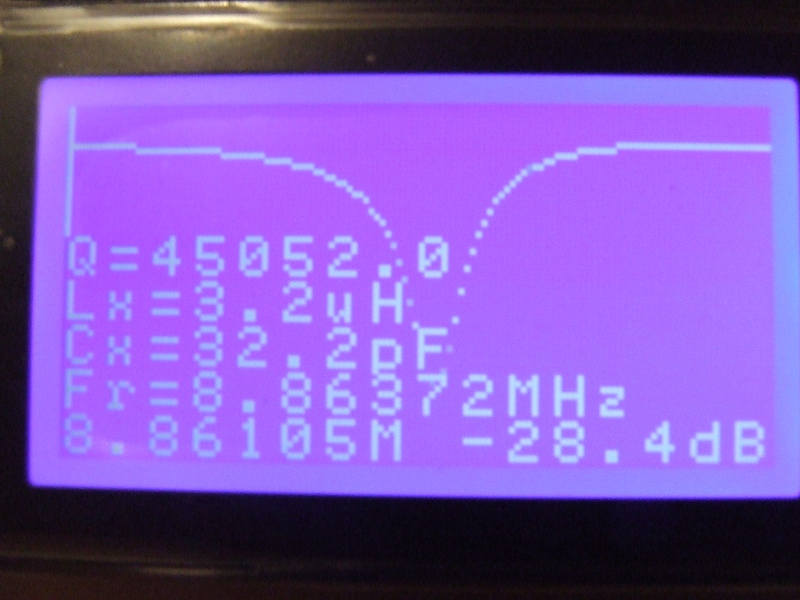
Przed pomiarem należy miernik skalibrować pamiętając, że w drugim kroku kalibracji, kiedy łączymy wejście z wyjściem, w tor pomiarowy musi być wpięta przystawka LCQ.
Na pokazanym rysunku zakres przemiatania to 5kHz. Mierzony rezonator pokazuje dołek rezonansu szeregowego a na ekranie pojawia się częstotliwość rezonansowa kwarcu Fr oraz dobroć Q. Inne zmienne na ekranie na razie nie mają znaczenia przy tym pomiarze. Dla przypomnienia, jeśli wykres nie leży na środku wykresu to można go przesunąć używając klawiszy (<-) lub (->) przesuwając pionowy wskaźnik częstotliwości w kierunku poza ekran.
Wpinając na skrajne złącza śrubowe przystawki LCQ drugi rezonator można łatwo uzyskać szybkie porównanie dwóch kwarców, te mające rozbieżność częstotliwości pokażą na wykresie dwa minima.
Budowa filtra kwarcowego - krok 2 - identyfikacja parametrów rezonatorów.
Do pomiarów użyte zostaną kwarce o częstotliwości nominalnej 8.867MHz i o takiej mniej więcej częstotliwości będzie nasz filtr kwarcowy przy dodatkowym założeniu, że zbudowany będzie tylko z 4 rezonatorów.
W tej fazie należy ustalić własności wyselekcjonowanych rezonatorów. Zbliżone wartości częstotliwości rezonansowej i dobroci zapewnią, że pozostałe parametry kwarców będą identyczne. Szukamy więc wartości L, Cs, Cp i R z pokazanego na początku modelu rezonatora i wystarczy to zrobić tylko dla jednego z rezonatorów.
W tym celu należy początkowo włączyć jeden z rezonatorów w tor pomiarowy szeregowo.

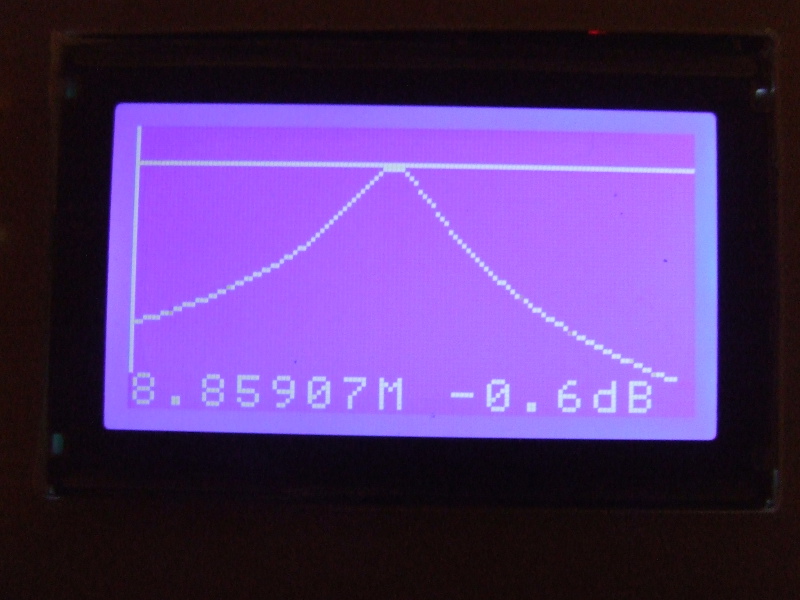
Nie zmieniając zakresu pomiarowego częstotliwości, mierzymy tłumienie transmisyjne kwarca za pomocą opcji "Pomiar -> Pomiar w pasmie". Ze względu na niewielkie wartości tłumienia kwarca włączonego szeregowo, warto w tym miejscu użyć właśnie opisanego wcześniej tłumika wyjściowego. Poprawi to rozdzielczość pomiaru. Na tej właśnie podstawie ustaliłem, że tłumienie to ma wartość ok. 0.7 dB a więc nieco więcej niż na pokazanym rysunku. Dla przypomnienia, wartość tłumienia odczytamy na dole z prawej strony ekranu przesuwając poziomą linię odniesienia za pomocą prawych klawiszy.
Kolejno trzeba ustalić częstotliwości rezonansowe: szeregową i równoległą kwarca. W tym celu zakres pomiarowy powinien być rozszerzony do mniej więcej 30-100kHz aby objąć na jednym wykresie oba rezonansy:
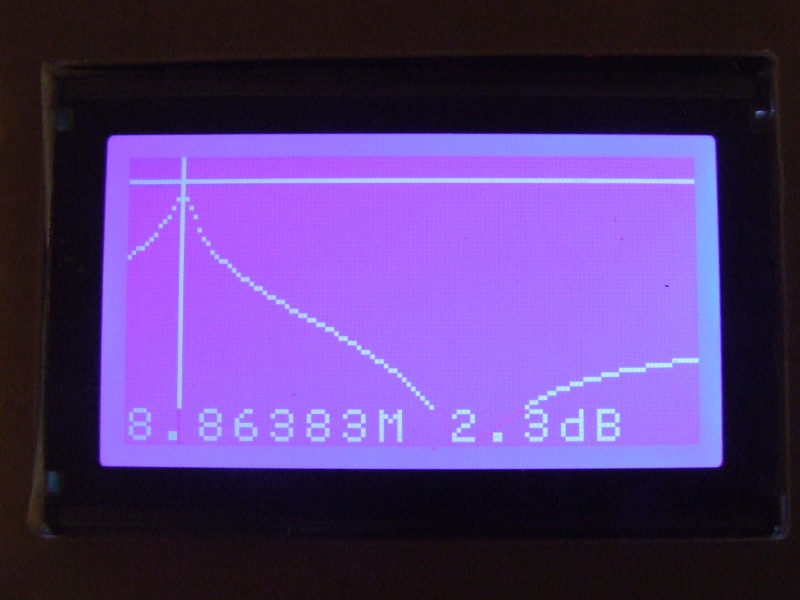
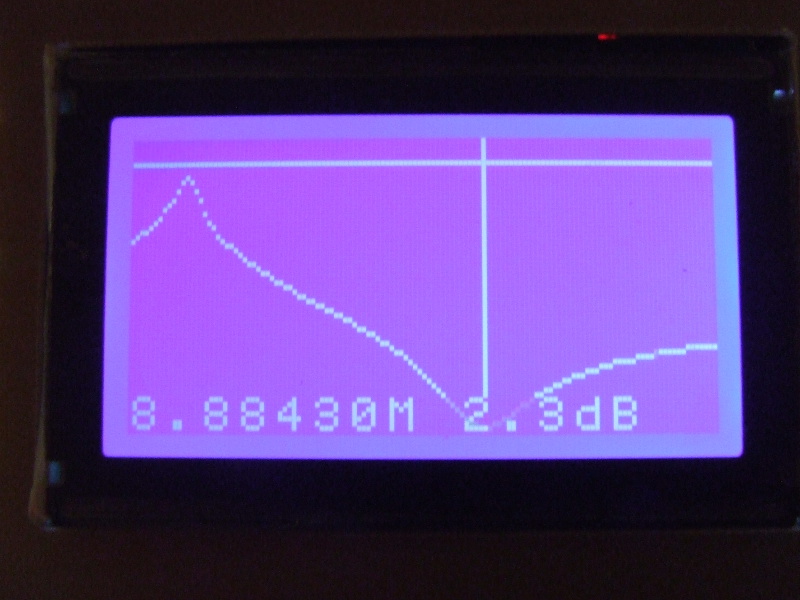
Ponieważ mierzymy kwarc włączony w tor pomiarowy szeregowo to rezonansowi szeregowemu odpowiada maksimum na wykresie a rezonansowi równoległemu minimum. Lewy (górny) rysunek wskazuje, że rezonans szeregowy to 8.8638MHz a prawy (dolny) rysunek pokazuje, że rezonans równoległy ma wartość 8.8843MHz. Oba rezonansy dzieli więc ponad 20kHz różnicy. Zanjomość wartości rezonansów jest niezbędna do ustalenia parametrów L i Cs a wartość tłumienia do ustalenia wartości R.
Pojemność Cp ustalić można przez bezpośredni pomiar - jeśli nasz miernik jest tak dokładny - tak jabky kwarc był zwykłym kondensatorem. Jednak z pomocą NA01/02 możemy Cp ustalić z dość dużą dokładnością metodą pośrednią. W tym celu należy przygotować jakąś cewkę o indukcyjności 5-20uH oraz znaną pojemność o niewielkiej wartości (3-10pF) - czyli o wartości zbliżonej do spodziewanej wartości Cp: ja użyłem kondensatora 4.7pF oraz cewki o 48 zwojach DNE0.4 na karkasie o średnicy ok. 11mm.

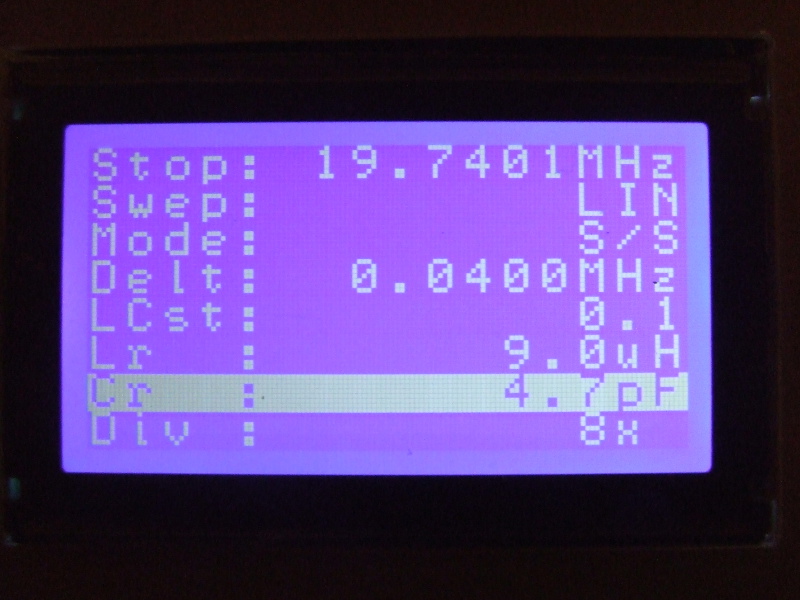
Zakładając, że pojemność jest wartością znaną, na początku, ustalę indukcyjność mojej cewki z pomocą przystawki LCQ. W tym celu, w menu pomiarowym należy ustawić w polu Cr wartość znanej pojemności czyli właśnie 4.7pF. Zakres przemiatania należy ustalić mniej więcej w zakresie 15-30MHz i następnie po skalibrowaniu miernika należy wykonać pomiar takiego obwodu rezonansowego za pomocą przystawki LCQ ("Pomiar -> Pomiar + Q"):


Jak widać cewka jest w rezonansie na częstotliwości ok. 17.959MHz co jest tu mniej istotne ale wyliczona wartość indukcyjności cewki, Lx, to 16.7uH. W kolejnym kroku cewka ta zostanie użyta do pomiaru rezonansu Cp kwarcu jako element odniesienia ale początkowo należy jej pomierzoną wartość wprowadzić jako Lr w głównym oknie pomiarowym. Nie ma tu zwykle potrzeby zmiany ani zakresu przestrajania ani ponownej kalibracji bo rezonans dla Cp powinien zmieścić się w ustawionym wcześniej zakresie.


Kolejno, zamiast kondensatora 4.7pF wstawiamy do pomiaru badany kwarc i odczytujemy dla rezonansu wartość Cx jako 4.5pF - jest to właśnie szukana wartość Cp naszego kwarca.

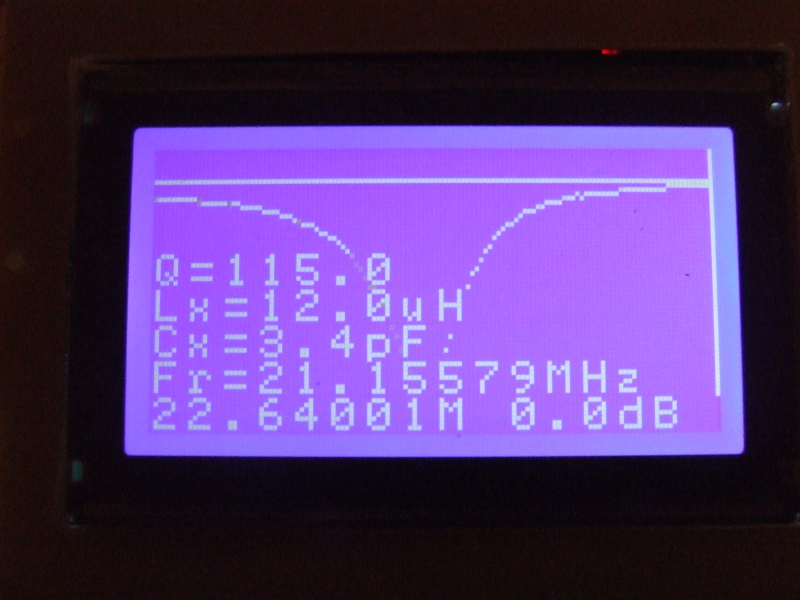
Podobny pomiar dla kwarca niskiego (w tym wypadku o częstotliwości 8MHz) dał wynik 3.4pF co się zgadza z intuicją. Mniejszy rezonator ma mniejsze pojemności związane z wymiarami fizycznymi obudowy.
Budowa filtra kwarcowego - krok 3 - wyliczenie parametrów zastępczych kwarca.
Na podstawie ustaleń z pomiarów jesteśmy gotowi do wyliczenia R, L oraz Cs (dla przypomnienia Cp znamy juz z pomiarów). Teraz do obliczeń należy zaprząc matematykę ale takie rzeczy zrobili już inni koledzy. Między innymi Alexander C. Frank (aka Ajarn Changpuak)
na swojej stronie
(
http://www.changpuak.ch/electronics/Quar...ner_1.php)
wykonał za nas czarną robotę oraz podał wzory na podstawie których udostępnił w sieci swój interaktywny kalkulator parametrów kwarców.
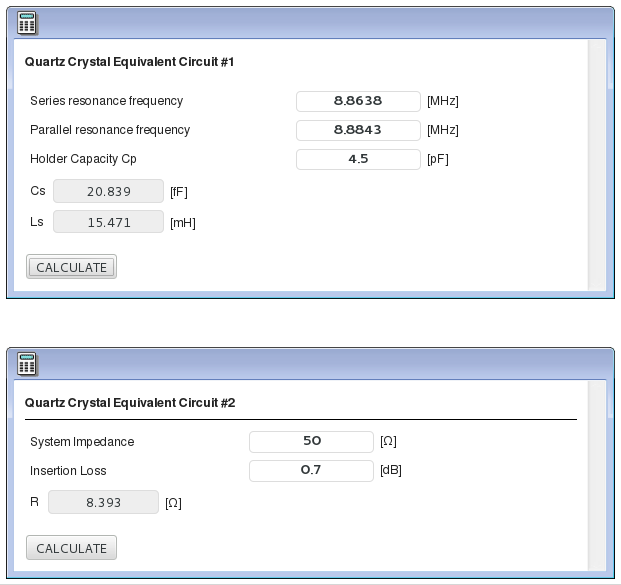
Kalkulator wylicza dla podanych danych, że L=15,471mH, Cs=20.839fF a R=8.393ohma. Do kompletu mamy jeszcze wcześniej znaną wartość Cp=4.5pF. Proszę zwrócić uwagę, że indukcyjność jest stosunkowo duża w stosunku do pojemności szeregowej Cs (liczona w femto faradach czyli 10-15F!). To właśnie, i mała oporność szeregowa w modelu potwierdzają, że kwarce mają tak dużą dobroć.
Wyliczone tu wartości zastepcze modelu użytego kwarcu są wystarczające do przejścia do kolejnej fazy projektowej czyli do wyliczenia elementów filtra drabinkowego oraz parametrów takiego filtra.
Budowa filtra kwarcowego - krok 4 - wyliczenie parametrów filtra kwarcowego.
Mając wyliczone parametry rezonatorów w filtrze można przystąpić do projektowania filtra. I znowu Alexander C. Frank (aka Ajarn Changp
na swojej stronie
http://www.changpuak.ch/electronics/Quar...gner_2.php
wykonał za nas czarną robotę.
Wpisujemy poszczególne dane modelu kwarca i przyjmujemy doadtkowe założenia, że częstotliwość filtra to częstotliwość rezonansu szeregowego kwarca, filtr złożony będzie z 4 kwarców z pasmem 2.4kHz a zafalowania w paśmie nie większe niż 0.5dB
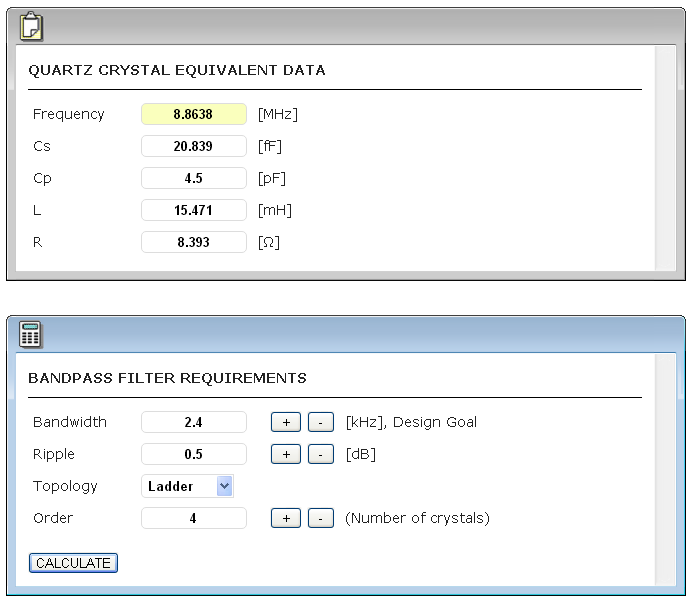
Dla takich danych otrzymujemy gotowe parametry filtra - tu pokazane na dwóch rysunkach ze względu na koniecznośc przewinięcia ekranu:
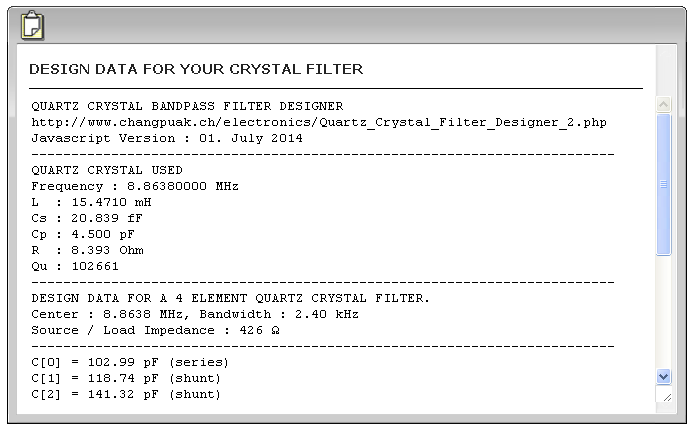
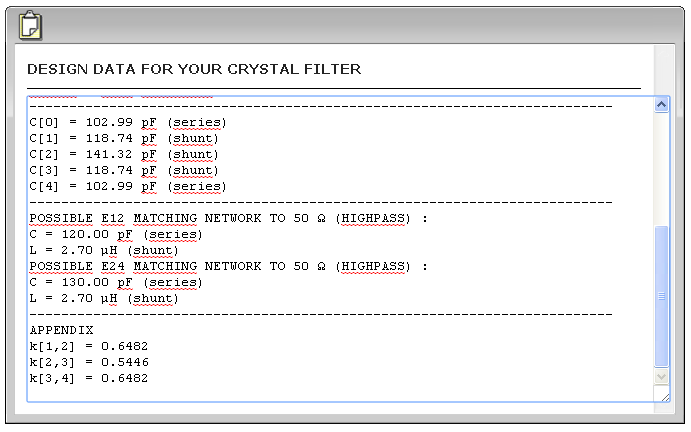
Najważniejsze są wartości pojemności szeregowych (serial) i równoległych (shunt) a także spodziewana impedancja. Tu uzyskaliśmy 426 omów impedancji dla filtra więc praca w sieci 50 omowej wymaga jakiegoś dopasowania. Ale podczas kalkulacji parametrów filtra uzyskujemy także informację o propozycji dopasowania za pomocą czwórnika gamma (czyli złożenia pojemności i indukcyjności o odpowiednich parametrach). Ponieważ filtr pracuje wąsko to dopasowanie powinno działać bez problemów. Obustronne dopasowanie filtra wymaga dodania elementów opisanych jako "POSIIBLE MATCHING TO 50 ohm" w formie czwórnika gamma z kondensatorem na zewnątrz filtra (HIGH PASS).
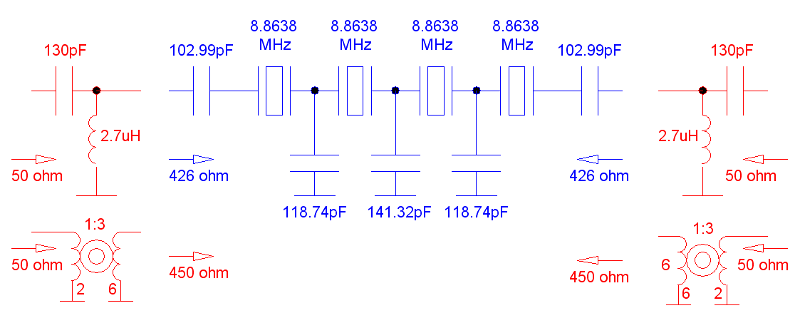
Alternatywą jest użycie transformatora o przekładni 1:3 co spowoduje przełożenie impedancji w relacji kwadratowej czyli uzyskamy zamiast 426 omów impedancję 450 omów (3^2*50omów=450omów) co jest wartością do zaakceptowania. Oba te sposoby pokazane zostały na schemacie filtra. Oczywiście w układzie transceivera łatwiej będzie dopasować filtr właśnie do impedancji 426 omów co wymaga odpowiedniego doboru punktu pracy tranzystora i lub oporników dopasowujących jeśli filtr pracował będzie pomiędzy układami scalonymi.
Na koniec warto by sprawdzić czy zaproponowany czwórnik gamma spełni swoją rolę i tym miejscu z pomocą może nam przyjść inny kolega z Internetu a właściwie cała firma: "TELESTRIAN", która udostępnia kalkulator dopasowania impedancji
z jednoczesnym obrazowaniem na wykresie Smitha
(
http://cgi.www.telestrian.co.uk/cgi-bin/...smiths.pl)
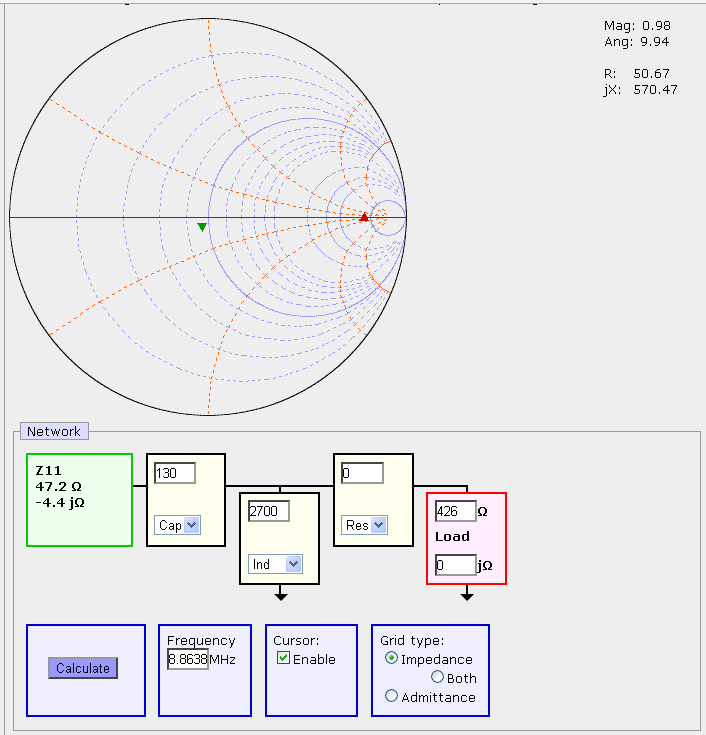
Kalkulator działa w ten sposób, że bada dopasowanie impedancji z prawej strony (kolor czerwony i tu wpisujemy nasze 426 omów) za pomocą czwórnika typu T a z lewej (zielonej) strony kalkulatora otrzymamy widzianą na zewnątrz impedancję. Dodatkowo, na wykresie Smitha uzyskamy wynik w formie dwóch kursorów, z których kursor czerwony to dopasowywana impedancja a kursor zielony pokazuje wynik dopasowania. Oczywiście dopasowanie idealne do sieci 50 omów jest wtedy kiedy kursor zielony znajdzie się w środku wykresu.
Ponieważ użyte dopasowanie jest typu gamma więc jedno z ramion czwórnika T powinno być zredukowane przez założenie, że ma charakter rezystancyjny i wartość 0. Ponieważ układ gamma ma być górnoprzepustowy to na zewnątrz ustawiamy kondensator szeregowy a do masy indukcyjność pamiętając, że wartość indukcyjności podaje się w tym przypadku w nH a więc nasze dopasowanie 2.7uH należy podać jako 2700.
Na obu stronach z kalkulatorami można ćwiczyć różne konfiguracje filtrów kwarcowych dla zdefiniowanego wcześniej układu zastępczego użytego filtra. Życzę więc miłej zabawy zarówno podczas pomiarów za pomocą NA01/02 jak i z kalkulatorami i czekam, że ktoś się pokusi o praktyczną realizację takiego projektu ;-)
L.J.