Witam!
Dziękuję za miłe słowa choć chyba jeszcze nie zasłużone :-(
Właśnie odkryłem błąd w zaprezentowanym oprogramowaniu, podczas korekty ręcznej L i C nie odświeżał się pomiar SWR przez co nie wiadomo było czy zmiana poprawia czy pogarsza stan dopasowania.
ant_tun011.hex (Rozmiar: 39.07 KB / Pobrań: 275)
Problem testowania zrobionego już oprogramowania jest niemal tak ważny jak samo oprogramowanie (jego funkcjonalność).
Wczoraj poprawiałem właśnie sterowanie ręczne, formatowałem wyniki dla wartości L i C i zmieniłem sposób odczytu SWR przez jego pominięcie przy zmianie L lub C.
Dziś robiąc testy dopasowania do różnych oporności obciążenia wykryłem błąd.
L.J.
Witam!
Pora na najciekawszą cześć tego zadania a mianowicie algorytm wyszukiwania najlepszego dopasowania.
Na początek kilka założeń:
- do dyspozycji jest 8 wartości pojemności: 0, 10, 22, 47, 100, 250, 500 i 1000pF z których można można ułożyć łącznie 2^7 czyli 128 różnych wartości pojemności od 0 do 1929pF a najmniejszy krok to 10pF.
- do dyspozycji jest 8 wartości indukcyjności: 0.16, 0.32, 0.64, 1.25, 2.5, 5.0 i 10uH z których można ułożyć łącznie 2^7 czyli 128 różnych wartości indukcyjności od 0 do 19,87uH a najmniejszy krok to 0.16uH.
- do dyspozycji są dwie konfiguracje Lmatch: LC do dopasowania w górę i CL do dopasowania w dół względem impedancji domyślnej -> 50 (51) omów.
- istnieje minimum SWR dla co najmniej jednej z kombinacji LC lub CL co nie oznacza jednocześnie, że to minimum będzie równe 1 (dla zbyt niskiej lub wysokiej częstotliwości lub zbyt małej lub dużej impedancji obciążenia)
Przewiduję sprawdzenie dwóch metod szukania najlepszego ustawienia, które opiszę poniżej z czego jedną z nich zastosowałem już w oprogramowaniu, jak się wydaje z, wstępnie, dobrym wynikiem.
A teraz kilka słów na temat ograniczeń. W tym wypadku podstawowym ograniczeniem są parametry przekaźników i czas. Zakłada się, że stabilizacja styków wymaga czasu ok. 20ms od momentu zadziałania przekaźnika. Użyte tu przekaźniki mają te czasy nieco lepsze ale do obliczeń założę właśnie 20ms.
Ilość możliwych ustawień LC lub CL dla 128 wartości C i L to 128*128=16384 kombinacji.
Najprostszą metodą sprawdzenia najlepszego ustawienia skrzynki byłoby przejrzenie wszystkich pomiarów i wybór tego, który jest najlepszy co wymaga ustawienia wszystkich możliwych kombinacji dla topologii LC i CL (nie znamy charakteru obciążenia) a czas jaki to zajmie wyniósłby co najmniej : 2*16384*20ms=655320ms czyli 655.36 sek (prawie 11 minut!).
Sprawdzenie wszystkich kombinacji i wybór najlepszej należy do grupy metod "brutal force". Przy zdefiniowanej i skończonej liczbie pomiarów wynik jest pewny (najlepszy ze wszystkich możliwych) ale czas potrzebny do jego realizacji dyskryminuje go w zastosowaniach praktycznych.
Dlatego jako pierwszą metodę jaką wprowadziłem do algorytmu jest metoda uproszczonego brutal force (Simplified Brutal Force - SBF -> moja inwencja nazewnicza). Algorytm SBF zakłada na początek sprawdzenie SWR dla wybranych wartości L i C oraz C i L a te wybrane wartości to właśnie wymienione na początku pojemności i indukcyjności użyte do montażu skrzynki.
Schematycznie można pokazać siatkę wartości L i C na płaszczyźnie jako 8*8 = 64 punkty. Dla takiej siatki zaznaczyłem wartości pojemności i indukcyjności podstawowych oraz przypisane im w programie wartości portów sterujących binarnie i w nawiasach dziesiętnie. Czerwony punkt to hipotetycznie miejsce najlepszego dopasowania.
Zakładając, że należy wykonać pomiary dla topologi LC jak i CL wymagane jest wykonanie 2*64=128 pomiarów w czasie 128*20ms=2560ms a więc nieco ponad 2.5 sek.
Po takim teście uzyskuje się dwie informacje: która z topologii LC czy CL ma zastosowanie oraz pierwsze przybliżenie najlepszego SWR (dla podstawowych wartości z szeregu L i C). Kolejne wyszukiwana będą odbywać się dla tak ustalonej topologii LC lub CL.
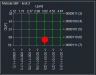
I właśnie dla ustalonej topologii oraz wstępnie określonych wartości L i C wykonuję drugi krok polegający na dokładniejszym przeszukaniu okolicy tych wartości (zarówno dla mniejszych jak i większych od nich) tak aby zakres przeszukiwań mniej więcej pokrywał się na brzegach z obszarami sąsiednich wartości podstawowych. I tu, w zależności od wybranych wstępnie L i C stosuję dodatkowe uproszczenie, nie przeszukuję wszystkich możliwych wartości ale w zależności od wartości wyjściowych L i C każdą, co drugą, co czwartą lub nawet co 16 wartość w ich otoczeniu. Zakładam przy tym ,że im większa wartość L lub C tym większe powinny być zmiany aby były zauważone przy obliczaniu SWR a poza tym rezonans (na jakim oparte jest dopasowanie LC/CL) zmienia się z pierwiastkiem iloczynu LC a więc zmiana 2 krotna częstotliwości rezonansu wymaga 4 krotnej zmiany L lub C.
Na pokazanym rysunku czerwony punkt to umownie optimum dopasowania a zielone pole to obszar poszukiwań po ustaleniu w kroku pierwszym, że topologia to LC a ustalone wartości wstępne to 47pF i 2.5uH.
W kroku drugim przeszukuję wybrany obszar dla C z krokiem 1 ale dla L już z krokiem 4. Gdyby w rzeczywistości minimum SWR było w miejscu oznaczonym czerwonym punktem wtedy zapewne algorytm znalazłby minimum dla 69pF i 3.62uH.
Drugi krok wymaga wykonania 7*5=35 pomiarów w czasie ok. 700ms a więc łączny czas przeznaczony na przekaźniki to dla tego przypadku ok. 3.25s, Biorąc pod uwagę także czas obliczeń procesora, to łączny czas działania skrzynki można określić na ok. 4 sek a samo dopasowanie wydaje się być zadowalające. W najgorszym przypadku algorytm potrzebuje niewiele więcej czasu na najdłuższe wyszukiwanie najlepszego ustawienia. Teoretycznie można zastosować kolejny krok zawężając obszar poszukiwań i używając najmniejszych możliwych zmian ale na razie nie wydaje mi się to konieczne.
Zastosowana topologia sprzętowa ułatwia programowanie. Zarówno pojemności jak i indukcyjności sterowane są z własnego, oddzielnego portu procesora w taki sposób, że najmniejszej wartości L i C przypisany jest bit 0 portu a największej bit 6. W ten sposób operacja shift rejestru portu w najtańszy (w sensie czasu) sposób umożliwia przegląd podstawowych wartości L i C a przeszukiwanie w drugim kroku prawdopodobnego obszaru minimum SWR można wykonać zakładając zmianę wartości dla odpowiedniego portu w zakresie od pewnej wartości minimalnej do pewnej wartości maksymalnej w sposób ciągły co bardzo łatwo realizuje operacja "for" z zadanym krokiem.
Tak więc algorytm nie jest specjalnie inteligentny (dlatego brutal force) ale jest na tyle uproszczony, że skutecznie redukuje ilość pomiarów do akceptowalnej wartości (dlatego uproszczony).
L.J.
Witam!
Drugi z proponowanych algorytmów wyszukiwania najlepszego ustawienia skrzynki nazwałem na potrzeby tego opisu jako uproszczona metoda gradientu (SGM).
Ale i w tym przypadku procedura szukania ustawienia zaczyna jak w poprzedniej metodzie od identyfikacji topologi (LC lub CL) oraz wyszukania najlepszego ustawienia dla podstawowych wartości L i C przez przeszukanie 2*64 ustawień jak w metodzie SBF.
W przeciwieństwie jednak do algorytmu SBF, tu procedura wykonuje naprzemiennie kroki w naprzemiennych kierunkach (mniejsze lub większe L lub C) tak jak pokazałem na rysunku. Zakładając, że startujemy z pojemnością w punkcie A badam SWR dla wartości w otoczeniu punktu A w górę (punkt B) oraz w dół (punkt C) i w zależności od wyniku pomiaru SWR wybieram punkt B jako lepszą kombinację w następnym kroku procedury. Kolejno robię to samo dla indukcyjności i wybieram lepszą z możliwości. Otwartą kwestią jest jaki powinien być krok przeszukiwania aby wyniki różniły się na tyle aby można było wybrać lepszą z nich.
Droga do rozwiązania optymalnego mogłaby wyglądać jak na kolejnym rysunku gdzie na czerwono oznaczyłem wybory gorsze a na żółto te prowadzące do lepszego wyniku. Wydaje się, że w tej metodzie można by uzyskać szybsze osiągnięcie rozwiązania optymalnego (mniejsza ilość sprawdzeń) ale do rozstrzygnięcia są następujące problemy:
- skok jednostkowy zmiany L i C - wydaje się, że im większa wartość L lub C tym skok powinien być większy
- zdefiniowanie kryterium zatrzymania procedury. Na razie przychodzi mi do głowy np. osiągnięcie SWR lepszego niż założony akceptowalny próg lub/i maksymalna ilość kroków (pomiarów) bo może się okazać, że w pobliżu minimum SWR wszystkie sąsiednie punkty będą miały identyczne wartości i algorytm będzie się kręcił w kółko.
Zakładam, że funkcja SWR, jako dwuargumentowa (L i C) ma jedno extremum globalne w obszarze zmienności L/C. Szukam rozwiązania analitycznego żeby pokazać tą zależność na jakimś ładnym wykresie ale byc może zrobię co najmniej wykres pomiarów dla obu kroków dla metody SBF.
W zastosowanej już procedurze SBF wynik jest jednoznaczny - najlepszy ze skończonego zbioru wykonanych pomiarów, w procedurze SGM zależy od doboru kroku pomiaru oraz założonego kryterium zakończenia poszukiwań.
A może macie inne propozycje?
L.J.
no ale chyba w tym przypadku tylko bardzo bliskie okolice dołka. Znając (zakładając) jakiś kształt okolic dolin i dołka można by coś podumać w temacie dobierania długości kroku.. Z drugiej strony może metoda SBF jest dobra dlatego że od razu szuka globalnego minimum, w metodzie gradientu wpadamy w długą i krętą dolinę którą potem wolno dochodzimy do właściwego minimum.